4(2a+3)<7-2a and represent on number line
Answers
representing the number on number line a < -1/2
How to find the number and represents the number on number line?The horizontal straight lines in mathematics known as number lines are where integers are arranged in equal intervals. A number line can be used to represent every number in a sequence.
given that
4(2a+3)<7-2a
firstly solve the equation so now multiply 4 with 2a and 3 .
8a + 12<7-2a
then move -2a to the left side and +12 to right side. then -2a changes to +2a and +12 changes to -12
8a + 2a < - 12 + 7
now add the values on both sides
10a < - 5
now divide the both sides by 10
\( \frac{10}{10} a < - \frac{5}{10} \)
\(a < - \frac{1}{2} \)
so ,
\(a < - \frac{1}{2} \)
Learn more about number line, refer :
https://brainly.com/question/24644930
#SPJ9

Related Questions
A right triangle has a hypotenuse of length 3.80 m, and one of its angles is 31.0°. What are the lengths of the following sides?

Answers
Answer:
• (a)The length of the side opposite 31.0° is 1.96 meters.
,• (b)The length of the side adjacent 31.0° is 3.26 meters.
Explanation:
In the right triangle:
• The length of the hypotenuse = 3.80 m
,• Let the side ,opposite ,angle 31.0° = x
• Let the side ,adjacent ,angle 31.0° = y
(a)
From trigonometric ratios:
\(\begin{gathered} \sin\theta=\frac{Opposite}{Hypotenuse} \\ \implies\sin31.0\degree=\frac{x}{3.80} \end{gathered}\)Cross multiply:
\(\begin{gathered} x=3.80\times\sin31.0\degree \\ x=1.9571 \\ x\approx1.96\;m \end{gathered}\)The length of the side opposite 31.0° is 1.96 meters.
(b)From trigonometric ratios:
\(\begin{gathered} \cos\theta=\frac{Adjacent}{Hypotenuse} \\ \implies\cos31.0\degree=\frac{y}{3.80} \end{gathered}\)Cross multiply:
\(\begin{gathered} y=3.80\times\cos31.0\degree \\ y=3.2572 \\ y\approx3.26\;m \end{gathered}\)The length of the side adjacent 31.0° is 3.26 meters.
Me ayudan por favor con estos ejercicios de álgebra con la 15, 16 y 17

Answers
Selena rides her bicycle to work . it takes her 15 minutes to go 3 miles . if she continues at the same rate , how long will it take her to go
Answers
Answer:
5 minutes per mile
Step-by-step explanation:
15 divided by 3 = 5
Let H be a solid hemisphere of radius 4 whose density at any point is proportional to its distance from the center of the base. (Let K be the constant of proportionality.) Find the mass of H.
Answers
The mass of the solid hemisphere H is 4πK.
To find the mass of the solid hemisphere H, we need to integrate the density over its volume and then multiply by the volume.
Let's set up the problem in spherical coordinates. In spherical coordinates, the density function can be written as ρ = Kr, where ρ is the density, K is the constant of proportionality, and r is the distance from the center of the base.
The volume element in spherical coordinates is given by dV = r^2 sin(θ) dr dθ dϕ, where r ranges from 0 to the radius of the hemisphere (4), θ ranges from 0 to π/2 (as we are dealing with the upper half of the hemisphere), and ϕ ranges from 0 to 2π.
Now, let's integrate the density over the volume of the hemisphere:
m = ∫∫∫ ρ dV
= ∫∫∫ K r (r² sin(θ) dr dθ dϕ)
= K ∫(0 to 2π) ∫(0 to π/2) ∫(0 to 4) r³ sin(θ) dr dθ dϕ.
Evaluating the innermost integral first:
∫(0 to 4) r³ dr = [r⁴/4] (0 to 4) = 4⁴/4 - 0 = 64.
Now we can substitute this result into the remaining double integrals:
m = K ∫(0 to 2π) ∫(0 to π/2) 64 sin(θ) dθ dϕ.
Evaluating the next integral:
∫(0 to π/2) sin(θ) dθ = [-cos(θ)] (0 to π/2)
= -cos(π/2) - (-cos(0))
= -(-1) - (-1) = 1 + 1 = 2.
Substituting this result into the final integral:
m = K ∫(0 to 2π) 2 dϕ
= 2K [ϕ] (0 to 2π)
= 2K (2π - 0)
= 4πK.
Therefore, the mass of the solid hemisphere H is 4πK.
To know more about integral check the below link:
https://brainly.com/question/27419605
#SPJ4
A rectangular paperboard measuring 20in long and 16in wide has a semicircle cut out of it, as shown below.Find the area of the paperboard that remains. Use the value 3.14 for pi, and do not round your answer. Be sure to include the correct unit in your answer.
Answers
Answer: 219.52 inch^2
Step-by-step explanation:
Given the dimensions of rectangular papaerboard:
Length = 20inches
Width = 16inches
Area of rectangle = Length × width
Area of rectangle = 20 × 16 = 320 in^2
Area of a circle = pi*r^2
Therefore, area of semicircle = (pi*r^2) / 2
Diameter of circle = width of rectangle = 16 inches
Radius = diameter / 2 = 16 /2 = 8inches
Therefore, area of semicircle = (pi*8^2) / 2
= (3.14 × 64) / 2
= 200.96 / 2
= 100.48 inch^2
Therefore, area of paperboard left :
Area of rectangle - area of semicircle
320 - 100.48
= 219.52 inch^2

(y+1)^5 divided by (y+1)^2
will mark brainliest
Answers
Answer:
(y+1)^3
Step-by-step explanation:
When dividing powers, subtract them. Therefore, 5-2 = 3. So, (Y+1)^5/(Y+1)^2 = (Y+1)^3
Focus point of (x+1/2)^2=20(y-5)
Answers
The focus point of the parabola defined by the equation (x + 1/2)² = 20(y - 5) is located at (-1/2, 10).
To find the focus point of the parabola defined by the equation (x + 1/2)² = 20(y - 5), we can compare it to the standard form of a parabola:
(x - h)² = 4p(y - k).
In the standard form, (h, k) represents the vertex of the parabola, and p represents the distance from the vertex to the focus.
Comparing the given equation to the standard form, we can identify that h = -1/2 and k = 5.
This means the vertex of the parabola is at the point (-1/2, 5).
Next, we need to determine the value of p, which represents the distance from the vertex to the focus.
In the standard form, 4p is equal to the coefficient of (y - k).
The coefficient is 20, so we have 4p = 20. Solving for p, we divide both sides by 4, giving us p = 5.
Since p represents the distance from the vertex to the focus, and p is equal to 5, we can conclude that the focus point of the parabola is located 5 units above the vertex.
Starting from the vertex (-1/2, 5), we move vertically upward by 5 units to find the focus point, which is at (-1/2, 10).
For similar questions on focus point
https://brainly.com/question/31452966
#SPJ11
Which of the following equations would be parallel to the line x = 3?
1. y = 3x
2. y = 1
3. y = x
4. x = 5
Answers
Answer:
4. x = 5
Step-by-step explanation:
For two lines to be parallel they must have the same slope, but not be the same line. Both x=3 and x=5 both have slopes of 0, so they are parallel. Another way to tell is that x=3 is a vertical line; therefore, it will be parallel to any other vertical line, such as x=5.
for the beam and loading shown, (a) draw the shear and bending-moment diagrams, (b) determine the equations of the shear and bending-moment curves. 5.1
Answers
Bending moment curve equation below point A will be:
M = 15x - 3x² for 0 ≤ x ≤ b
Determination of shear and bending moment curves.
For the beam and loading shown, we can do the following:
Equation of shear curve (above point A):V = RA - w.x
For x = a,V = RA - w.a
For x = b,V = RA - w.b
Since the loading is symmetric, RA = w(a + b) / 2= (6 * 5) / 2= 15kNV = 15 - 6a for a ≤ x ≤ b
Equation of shear curve (below point A):
V = RA - w.x
For x = 0,V = RA - w.0RA = w(a + b) / 2= (6 * 5) / 2= 15kNV = 15k for 0 ≤ x ≤ a
The shear curve equation becomes;
V = 15k for 0 ≤ x ≤ a
V = 15 - 6a for a ≤ x ≤ b
Equation of bending moment curve (above point A):
M = RAx - ½w.x²For 0 ≤ x ≤ a,
M = 15x - ½(6x²) = 15x - 3x²For a ≤ x ≤ b,
M = 15x - 6a(x - a) - ½(6x²)= 15x - 6ax + 6a² - 3x²
The bending moment curve equation above point A becomes:
M = 15x - 3x² for 0 ≤ x ≤ a
M = 15x - 6ax + 6a² - 3x² for a ≤ x ≤ b
Equation of bending moment curve (below point A):
M = RAx - ½w.x²For 0 ≤ x ≤ b,
M = 15x - ½(6x²) = 15x - 3x²
The bending moment curve equation below point A becomes;
M = 15x - 3x² for 0 ≤ x ≤ b
Learn more about Bending Moment.
brainly.com/question/30242055
#SPJ11
4. Solve 5x + 25 = 250 x = ?* Enter the number value only.
Answers
Answer: x = 5/49 ; 0.102041
Step-by-step explanation:
Subtract 5x on both sides. 25 = 245xDivide by 245 on both sides. x = 5/49. As a decimal, it is approximately 0.102041.∛a² does anyone know it
Answers
The equivalent expression of the rational exponent ∛a² is \((a)^{\frac{2}{3}\).
What is a rational exponent?Rational exponents are exponents that are fractions, where the numerator is a power and the denominator is a root.
So rational exponents (fractional exponents) are exponents that are fractions or rational expressions.
To determine the rational exponent equivalent to the expression given, we will apply the power rule of indices as shown below.
The given expression is ;
∛a²
The rational exponent is calculated as follows;
∛a² = \((a)^{\frac{2}{3}\)
Thus, based on exponent power rule, the given expression is equivalent to ∛a² = \((a)^{\frac{2}{3}\)
Learn more about rational exponents here: brainly.com/question/30603002
#SPJ1
The complete question is below:
Find the equivalent expression of the rational exponent ∛a². does anyone know it
Factor: 3x3 + 15x2 +4xy +20y
Answers
Answer:
The factored version of the given equation is going to be (3x² + 4y)(x + 5)
Step-by-step explanation:
3x³ + 15x² + 4xy + 20y
First, you break down 3x³. You can do this by finding the common factor of 3x³ and 15x². You can add the x to the other parentheses because x times x² equals x³
(3x² + )(x + 5)
Now, we break down 4xy by finding the common factor of 4xy and 20y.
(3x² + 4y)(x + 5)
So, the factored version of the equation above is (3x² + 4y)(x + 5)
Help Will give crown
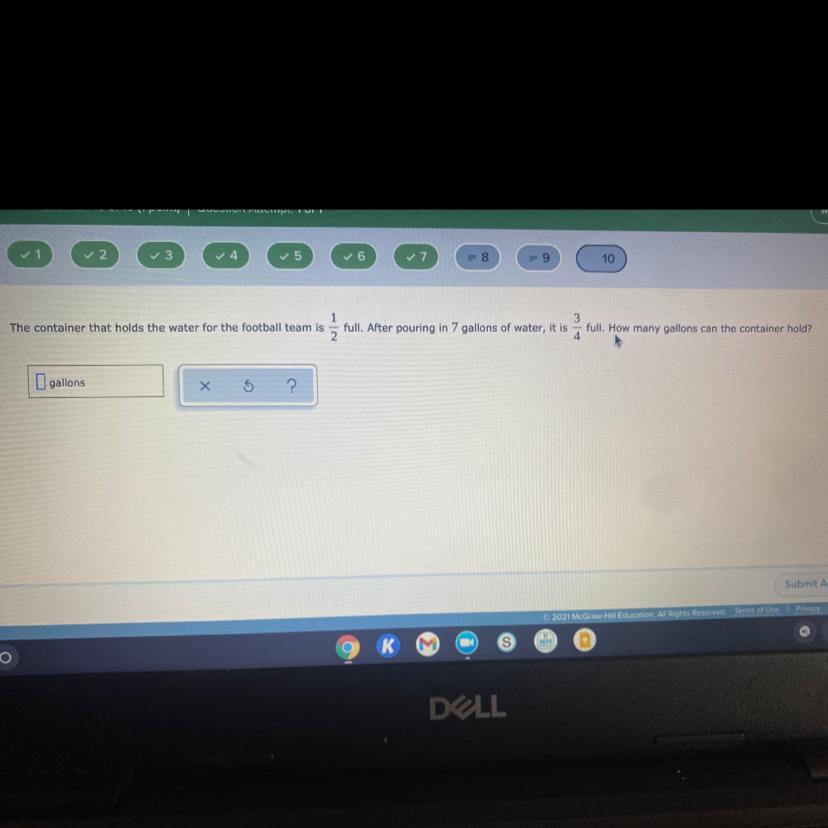
Answers
the answer is actually 4/6 pls give branliest and thanks
Answer:
28 gallons
Step-by-step explanation:
50% full
50% + 7 gallons = 75%
50% + 25% = 75%
25% = 7 gallons
\(\frac{25}{100}= \frac{7}{y}\)
25 × y = 100 × 7
25y = 700
25y ÷ 25 = 700 ÷ 25
y = 28
please i need help!!!

Answers
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Answer: Y-intercepts
Explanation:
I hope this helped!
<!> Brainliest is appreciated! <!>
- Zack Slocum
*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆*――*☆**☆*――*☆*――*☆*――*☆
Can somebody help me with the geometry equation.

Answers
Answer:
\(m\widehat{VU}=120^{\circ}\)
Step-by-step explanation:
The angle \(\angle TUV\) forms arc \(\widehat{TV}\). The measure of this arc is twice the measure of angle \(\angle TUV\), since \(U\) is a point on the circle. Since \(\overline{TU}\) forms an arc \(\widehat{TU}\), we can set up the following equation:
\(\widehat{TV}+\widehat{VU}=\widehat{TU}\).
Since arc TU represents half of a circle and there are 360 degrees in a circle, we can substitute the following values and solve for the measure of arc VU:
\(\\2\cdot 30^{\circ}+\widehat{VU}=180^{\circ},\\60^{\circ}+\widehat{VU}=180^{\circ},\\m\widehat{VU}=\boxed{120^{\circ}}\)
the value of n is a distance of 3 units from 1 1/2
Answers
Answer:
3
Step-by-step explanation:
Given the question :
The value of n is a distance of 3 units from 1 an 1/2 on a number line click on the number line to the possible values of n
From the context of the expression:
n is the distance which exists between 1 1/2 and 3 units from it;
Which may be ;
1 1/2 - - - - (1 1/2 + 3) = 4 1/2
1 1/2 - - - - - (3 - 1 1/2)
Either way, there exists a distance of 3 units between 1 1/2 and 3 units from it.
Hence, n = 3
find the distance between u= 0 −6 3 and z= −2 −1 8 .
Answers
The distance between the points u= 0 −6 3 and z= −2 −1 8 is approximately 9.95 units.
To calculate the distance between two points in three-dimensional space, we can use the distance formula, which is derived from the Pythagorean theorem. The distance formula states that the distance between two points (x1, y1, z1) and (x2, y2, z2) is equal to the square root of [(x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2].
Using this formula, we can find the distance between u and z as follows:
d = sqrt[(-2 - 0)^2 + (-1 - (-6))^2 + (8 - 3)^2]
= sqrt[4 + 25 + 25]
= sqrt(54)
≈ 9.95
Therefore, the distance between the points u and z is approximately 9.95 units.
Learn more about Distance:
brainly.com/question/15172156
#SPJ11
central high school is competing against northern high school in a backgammon match. each school has three players, and the contest rules require that each player play two games against each of the other school's players. the match takes place in six rounds, with three games played simultaneously in each round. in how many different ways can the match be scheduled?
Answers
The match can be scheduled in 900 different ways with the help of permutations and combinations.
Given,
Number of players from each school = 3.
Let, the players of the first school be A, B, and C.
Let, the players of the second school be X, Y, and Z.
The problem can be solved in two cases,
Case-1
According to the question,
Each player from the first school has to play twice with each player from the second school.
We can organize the schedule into six different rounds, i.e.,
Round 1 : AX BY CZ
Round 2 : AX BZ CY
Round 3 : AY BX CZ
Round 4 : AY BZ CX
Round 5 : AZ BX CY
Round 6 : AZ BY CX
In other words, we have to permutate these 6 rounds, i.e., 6! = 720 ways.
Case-2
Given,
Three rounds are played simultaneously in each round.
(a)
Round 1 : AX BZ CY
Round 2 : AX BZ CY
Round 3 : AY BX CZ
Round 4 : AY BX CZ
Round 5 : AZ BY CX
Round 6 : AZ BY CX
(b)
Round 1 : AX BY CZ
Round 2 : AX BY CZ
Round 3 : AY BZ CX
Round 4 : AY BZ CX
Round 5 : AZ BX CY
Round 6 : AZ BX CY
The total number of permutations for Case-2 will be twice of 6! / (2! 2! 2!), which is equal to 90+ 90 = 180.
Thus, the total number of ways in which the match can be scheduled is 720 + 180 = 900.
To learn more about permutations,
https://brainly.com/question/14767366
Can someone please help me with this? It's the only question I need help with (since we are reviewing things that we learned in 6th grade again)

Answers
Answer: 18 mega rolls
Step-by-step explanation:
Answer:
the second one is a better deal.
Step-by-step explanation:
first deal:
6 rolls for 9.24
9.24/6 = 1.54
1.54$ per roll
second deal:
18 rolls for 27.54
27.54/18 = 1.53
1.53$ per roll
the second one is one cent cheaper
among the six who are taking the test for the first time. (a) What kind of a distribution does X have (name and values of all parameters)? nb(x;6, 18
8
)
h(x;6,8,18)
h(x;6, 18
8
)
b(x;6, 18
8
)
b(x;6,8,18)
nb(x;6,8,18)
(b) Compute P(X=2),P(X≤2), and P(X≥2). (Round your answers to four decimal places.) P(x=2)=1
P(x≤2)=1
P(x≥2)=
(c) Calculate the mean value and standard deviation of X. (Round your answers to three decimal places.) mean individuals standard deviation individuals
Answers
The distribution for X is a negative binomial distribution, denoted as nb(x;6, 188), with parameters r = 6 (number of successes), p = 8/18 (probability of success in each trial).
To compute the probabilities:
P(X = 2): nb(2;6, 8/18)
P(X ≤ 2): nb(0;6, 8/18) + nb(1;6, 8/18) + nb(2;6, 8/18)
P(X ≥ 2): 1 - P(X < 2) = 1 - P(X ≤ 1)
To calculate the mean value and standard deviation of X:
Mean (μ) = r * (1 - p) / p
Standard Deviation (σ) = sqrt(r * (1 - p) / (p^2))
learn more about negative binomial distribution
brainly.com/question/32308397
#SPJ11
Rewrite each equation in factored form and solve using zero product property. Find the solutions of each equation. Use the notes about r * k = c and r + k = b. In the first problem c is 6 and b is -7. So you need the same r and k that multiply to be 6 but also add to be -7. The numbers you find will be the solutions

Answers
The factored form of the equation are as follows;
(d - 6)(d - 1) = 0(x + 9)(x + 9) = 0(u + 12)(u - 5) = 0How to write equation in factored form?Converting a quadratic function to factored form is called factoring.
Therefore,
let's factor the equation,
a.
d² - 7d + 6 = 0
d² - d - 6d + 6 = 0
d(d - 1) - 6(d - 1) = 0
(d - 6)(d - 1) = 0
b.
x² + 18x + 81 = 0
x² + 9x + 9x + 81 = 0
x(x + 9) + 9(x + 9) = 0
(x + 9)(x + 9) = 0
c.
u² + 7u - 60 = 0
u² - 5u + 12u - 60 = 0
u(u - 5) 12(u - 5) = 0
(u + 12)(u - 5) = 0
learn more on equation here: https://brainly.com/question/12055751
#SPJ1
Manny's Bakery recently spent a total of $600 on new equipment, and their average hourly operating costs are $5. Their average hourly receipts are $35. The bakery will soon make back the amount it invested in equipment. What would the total expenses and receipts both equal?Write a system of equations, graph them, and type the solution.
Answers
We are given taht a bakery has expenses that equal a fixed cost of $600 plus $5 for every hour of operating cost, this means that the expenses "E" are given by:
\(E=600+5h\)Where:
\(\begin{gathered} E=\text{ expenses} \\ h=\text{ operating hours} \end{gathered}\)We are also given that the receipts are $35 per hour, therefore, the receipts are given by:
\(R=35h\)We get the system of equations:
\(\begin{gathered} E=600+5h,(1) \\ R=35h,(2) \end{gathered}\)Now, we want to determine where both equations will have the same value. To do that we graph both equations and determine their point of minterception, as follows:
By graphing both equations we have obtained that the Expenses "E" and the Receipt "R" will intercept at the point
\((20,700)\)Where 20 represents the number of hours and 700 the total expenses and receipts.
Therefore, they both have the same value of $700.

AM NEVOIE DE REZOLVARE URGENT!!!
Answers
Answer:
it won't let me download. I'm sorry have a nice day
I don’t have a question but both of the answers are wrong i just did it right now and i got it wrong but it said the answer is 6

Answers
(WORK SHOWN BELOW)

Answer:
ok
Step-by-step explanation:
Solve for x 4x+8=6x−1 Give your answer as an improper fraction in its simplest form.
Answers
Answer:
Step-by-step explanation:
4x+8=6x-1
-4x . =-4x .
8 = 2x-1
-1+8=2x-1+1
7=2x
7/2= 2x/2
3.5=x
The value of x will be;
⇒ x = 9/2
What is an expression?
Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The expression is,
⇒ 4x + 8 = 6x - 1
Now,
Solve the expression for x as;
⇒ 4x + 8 = 6x - 1
Subtract 6x both side, we get;
⇒ 4x + 8 - 6x = 6x - 1 - 6x
⇒ - 2x + 8 = - 1
Subtract 8 both side,
⇒ - 2x = - 1 - 8
⇒ - 2x = - 9
Divide by - 2 as;
⇒ x = 9/2
Thus, The value of x will be;
⇒ x = 9/2
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ2
Which choice is the value of two over five raised to the second?
four over twenty-five
two over twenty-five
two over ten
four over seven
Answers
explanation:
Exponentiation: 2/5^ 2 = 22/5^2 = 4/25
2/5^2 = 4/25 = 0.16
1. Adam has $2 and is saving $2 each day. Brodie has $8 and is spending $1 each day After how many days will each person have the same amount of money?
A. 5x + 4 = 3x - 2
B. 3x + 6 = -2x + 1
C. 2x + 2 = -x + 8
D. x + 8 = 2x + 7
2. A number increased by 8 is equal to twice the same number increased by 7.
A. 5x + 4 = 3x - 2
B. 3x + 6 = -2x + 1
C. 2x + 2 = -x + 8
D. x + 8 = 2x + 7
Answers
1. After 2 days, both Adam and Brodie will have the same amount of money.
2. The number is -6.
1. Let's represent the number of days as 'x'.
Adam starts with $2 and saves $2 each day, so his total amount of money after 'x' days is 2 + 2x.
Brodie starts with $8 and spends $1 each day, so his total amount of money after 'x' days is 8 - x.
We want to find the number of days when both Adam and Brodie have the same amount of money:
2 + 2x = 8 - x
Adding 'x' to both sides, we get:
2 + 3x = 8
Subtracting 2 from both sides, we get:
3x = 6
Dividing both sides by 3, we get:
x = 2
2. Let's represent the number as 'x'.
The number increased by 8 is equal to twice the same number increased by 7:
x + 8 = 2(x + 7)
Expanding the equation, we get:
x + 8 = 2x + 14
Subtracting 'x' from both sides, we get:
8 = x + 14
Subtracting 14 from both sides, we get:
-6 = x
In the first problem, we set up equations to represent the amount of money Adam and Brodie have after 'x' days. By equating the expressions and solving for 'x', we found that it takes 2 days for both of them to have the same amount of money. Therefore, the correct answer is D. x + 8 = 2x + 7.
In the second problem, we set up an equation to represent the relationship between a number and twice that number increased by 7. By solving the equation, we found that the number is -6. Therefore, the correct answer is D. x + 8 = 2x + 7.
For more such questions on number
https://brainly.com/question/24644930
#SPJ8
Can someone help me please I need to turn this in tomorrow

Answers
Answer:
1. 24 different 4-digit numbers can be formed.
Step-by-step explanation:
2. The probability that the number 3 will be the first or third digit is 1:1, which is equal to 1/2 and 50%
3. The probability is 3:1, 3/4, or 75%
4. What is the probability that the first digit will be the number 3 and the second digit will be the number 7? Answer: 1/12
Pls help with this problem
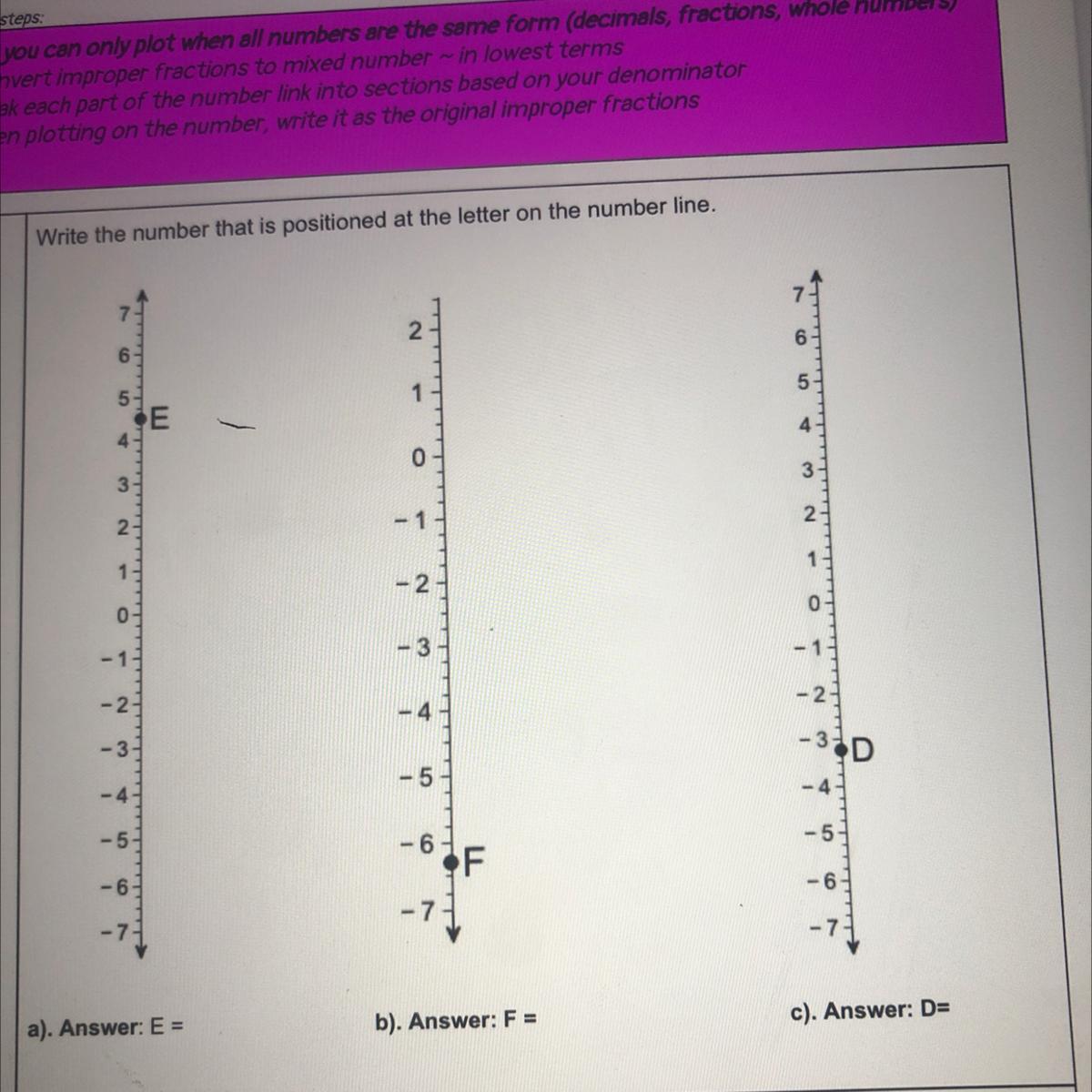
Answers
Answer:
E = 4.5, F = -6.25, D = -3.25
Step-by-step explanation:
the length of a rectangle is 3n+ 2 and its width is n-1. The perimeter of the rectangle is twice the sum of its length and its width.
Find the perimeter of the rectangle when n = 4 inches.
Answers
Answer:
34 inches
Step-by-step explanation:
3n+ 2 when n=4 would be equal to 14, and n-1 when n is 4 would be 3. 14+3=17, and 17x2= 34.
hope this helps!
ibrahim
Answer:
34 inches
Step-by-step explanation:
Substitute n with 4.
3*4+2= 14 (length)
4-1= 3 (width)
Since a rectangle has 4 sides, add two lengths (14*2) and two widths, (3*2)
28+6= 34