wait what about not in decimal form?
Answers
Answer:
don't know which question?
Step-by-step explanation:
¿???????
Related Questions
I need help with this practice problem I’m having trouble

Answers
Part N 1
\(2^{(6\log _22)}=12\)Apply property of log
\(\log _22=1\)so
\(\begin{gathered} 2^{(6\cdot1)}=12 \\ 2^6=12\text{ -}\longrightarrow\text{ is not true} \end{gathered}\)the answer is false
Part N 2
we have
\(\frac{1}{4}\ln e^8=\sqrt[4]{8}\)applying property of log
\(\frac{1}{4}\ln e^8=\frac{8}{4}\ln e=2\ln e=2\)so
\(2=\sqrt[4]{8}\text{ ---}\longrightarrow\text{ is not true}\)the answer is false
Part N 3
we have
\(10^{(\log 1000-2)}=10\)log1000=3
so
log1000-2=3-2=1
10^1=10 -----> is true
the answer is truePllls Help ill give brainliesstttt

Answers
Number one is 16
number two is 30
Number 3 is 100
Number four is 50
NO LINKS!! URGENT HELP PLEASE!!
Using the information given in each diagram below, decide if any triangles are congruent, similar but not congruent, or similar. If you claim the triangles are congruent or similar, create a flowchart justifying your answer. Part 1
Please help me with #22 and 24

Answers
Answer:
22. Congruent traingle
24. Similar traingle
We need to compare their corresponding sides and angles to determine if the two triangles are congruent or similar.
Attached flowchart to help you determine if two triangles are congruent or similar: See Attachment:
Properties of the similar triangle:
Corresponding angles are congruent: The corresponding angles of similar triangles are congruent. This means that if we label the corresponding angles of two similar triangles as A, B, and C and A', B', and C', respectively, then angle A is congruent to angle A', angle B is congruent to angle B', and angle C is congruent to angle C'.Corresponding sides are proportional: The corresponding sides of similar triangles are proportional. This means that if we label the corresponding sides of two similar triangles as a, b, and c and a', b', and c', respectively, then a:b::a':b' and b:c::b':c'.Ratios of corresponding sides are equal: The ratios of the corresponding sides of similar triangles are equal. This means that a/b = a'/b' and b/c = b'/c'.Perimeters and areas are proportional: The perimeters of similar triangles are proportional to the ratios of their corresponding sides, and the areas are proportional to the ratios of their corresponding sides squared. For example, if the ratio of the corresponding sides of two similar triangles is 2:3, then the ratio of their perimeters is also 2:3, and the ratio of their areas is 4:9.Height and base are proportional: The height of similar triangles is proportional to the ratios of their corresponding sides. This means that if two similar triangles have heights h and h', respectively, and corresponding sides a and a', then h/h' = a/a'. Similarly, if the triangles have bases b and b', then the ratio of their heights is also b/b'.Properties of the Congruent Triangle:
Corresponding sides and angles are congruent: In congruent triangles, corresponding sides and angles are congruent. This means that if we label the corresponding angles of two congruent triangles as A, B, and C and A', B', and C', respectively, then angle A is congruent to angle A', angle B is congruent to angle B', angle C is congruent to angle C', and side AB is congruent to side A'B', side AC is congruent to side A'C', and side BC is congruent to side B'C'.Congruent triangles have equal perimeters: Congruent triangles have the same size, so their perimeters are equal.Congruent triangles have equal areas: Congruent triangles have the same size, so their areas are equal.The sum of interior angles is always 180 degrees: The sum of the three interior angles of a triangle is always 180 degrees, regardless of whether the triangle is congruent or similar.The altitude, median, and angle bisector of a triangle are also congruent: In congruent triangles, the altitude, median, and angle bisector of one triangle are congruent to the corresponding altitude, median, and angle bisector of the other triangle.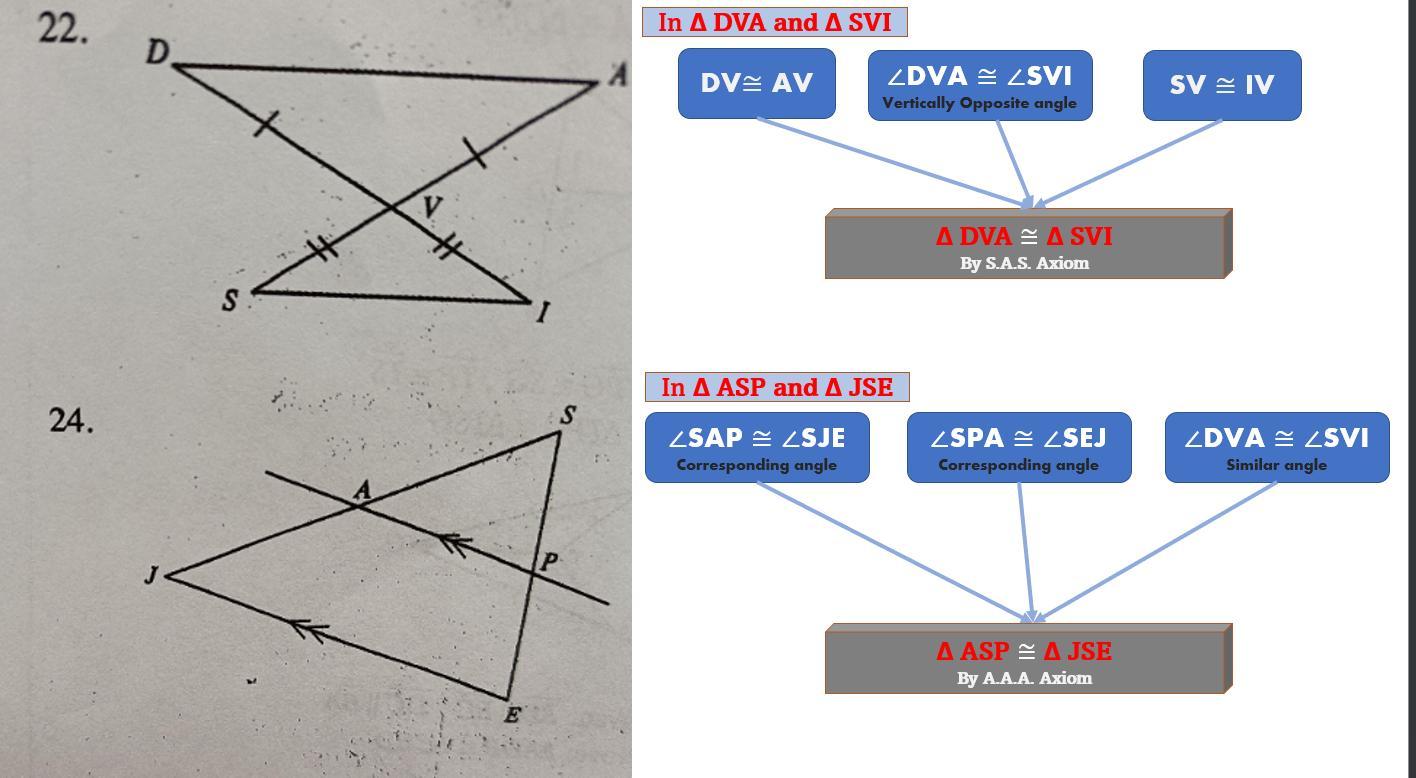
What is the value of 36x-8y² when x = 3 and y= 6
Answers
Answer:
-180
Step-by-step explanation:
just simply put the values in place of variables and solve
36(3) - 8(6)^2
108 - 8(36)
108 - 288
-180
Answer:
-180
Step-by-step explanation:
Plug in the variable numbers: \(36(3) - 8(6)^{2}\) 36 × 3 = 108Plug 108 in: \(108 - 8(6)^{2}\) \(6^{2}\) = 6 × 6 = 36Plug 36 in: \(108 - 8(36)\) 8 × 36 = 288Plug 288 in: 108 - 288108 - 288 = -180I have this question on an assignment and my calculator won't show the horizontal asymptote correctly can I get some help here?
Answers
What's the question? I can try and help..
the Cowboys have a record of 16 wins to 4 losses. The
Texans have a record of 18 wins to 3 losses. Which team
has a better record
Answers
Step by Step Explanation: To find which team is better you have to make there w/l's simplified, you do that by dividing 16 by 4 making the Cowboys winning 4 games per lose; then the Texans, 18 divided by 3 that makes the Texans win 6 times per lose so the Texans are better.
HELPPPPPPPPP AAAAAAAAA

Answers
Answer:
(5, -1)
Step-by-step explanation:
Equation 1: 3x + y = 14
Equation 2: 2x - 2y = 12
Rewrite equation 1 to make y the subject:
⇒ y = 14 - 3x
Substitute this into equation 2 and solve for x:
⇒ 2x - 2(14 - 3x) = 12
⇒ 2x - 28 + 6x = 12
⇒ 8x - 28 = 12
⇒ 8x = 40
⇒ x = 5
Substitute found value for x into either equation and solve for y:
using equation 1:
⇒ 3(5) + y = 14
⇒ 15 + y = 14
⇒ y = -1
Therefore, the solution to the system is (5, -1)
I just need help shouldn't be too hard if you understand it

Answers
Answer:
x =|y| x right = negative x left=+ y up = + y down = -
Karen, Dan, Dana, and Randi own a pizza shop. Karen and Dan each own 2/7 of the restaurant. The remaining share is owned equally between Dana and Randi. Exactly what fraction of the restaurant does Dana own?
Answers
The fraction of the restaurant that is owned by Dana, given the share owned by Karen and Dan is 3 / 14
How to find the fraction owned?First, find the fraction of the restaurant that is left to Dana and Randi after Karen and Dan's shares.
The fraction of the restaurant owned by both Dana and Randi are:
= Total ownership share - Fraction owned by Karen - Fraction owned by Dan
= 1 - 2/7 - 2/7
= 3/7
Dana and Randi share this equally so the fraction owned by Dana is:
= 3 / 7 ÷ 2
= 3 / 7 x 1/2
= 3 / 14
Find out more on fraction owned at https://brainly.com/question/17714269
#SPJ1
Given f(x) = x² - 5x - 6 and g(x) =
x² - 6x, what are the domain restrictions
for (-)(x)?
A) x # +6
B) x = 0
C) x = 0,6
D) x = -2,6
Answers
The domain restrictions for (f/g)(x) are (c) x = 0, 6
How to determine the domain restrictions for (f/g)(x)?From the question, we have the following parameters that can be used in our computation:
f(x) = x² - 5x - 6
g(x) = x² - 6x
The composite function (f/g)(x) is calculated as
(f/g)(x) = f(x)/g(x)
substitute the known values in the above equation, so, we have the following representation
(f/g)(x) = (x² - 5x - 6 )/(x² - 6x)
For the domain restriction, we have
x² - 6x = 0
When solved, we have
x = 6 or x = 0
Hence, the domain restrictions for (f/g)(x) are (c) x = 0, 6
Read more about domain at
https://brainly.com/question/27910766
#SPJ1
Question
Given f(x) = x² - 5x - 6 and g(x) = x² - 6x, what are the domain restrictions
for (f/g)(x)?
A) x = +6
B) x = 0
C) x = 0,6
D) x = -2,6
A recipe for 45 biscuits uses
5
2
cups of flour. How many biscuits are made from each cup of flour?
Answers
Answer:
18
Step-by-step explanation:
Please give brainliest!
Answer:
18
Step-by-step explanation:
Calc II Question
Sketch the region enclosed by the given curves and find its area.
Y = lxl , y = x^2 - 2
Answers
Answer:
\(\displaystyle A=\frac{20}{3}\)
Step-by-step explanation:
\(\displaystyle A=\int^2_{-2}(|x|-(x^2-2))\,dx\\\\A=2\int^2_0(x-(x^2-2))\,dx\\\\A=2\int^2_0(-x^2+x+2)\,dx\\\\A=2\biggr(-\frac{x^3}{3}+\frac{x^2}{2}+2x\biggr)\biggr|^2_0\\\\A=2\biggr(-\frac{2^3}{3}+\frac{2^2}{2}+2(2)\biggr)\\\\A=2\biggr(-\frac{8}{3}+2+4\biggr)\\\\A=2\biggr(-\frac{8}{3}+6\biggr)\\\\A=2\biggr(\frac{10}{3}\biggr)\\\\A=\frac{20}{3}\)
Bounds depend on whether you use -x or +x instead of |x|, but you double regardless. See the attached graph for a visual.

Which is the correct equation for a line that passes through the points (-2,7) and (2,-5)?
y=3x+5
y=1/3x+3
y= -3x-12
y= -3x+1
Answers
Answer:
y= -3x+1
Step-by-step explanation:
x1= -2 x2=2 y1=7 y2=-5
using the formula
(y-y1)/(x-x1)=(y2-y1)/(x2-x1)
(y-7)/(x-(-2))=(-5-7)/(2-(-2))
(y-7)/(x+2)=(-5-7)/(2+2)
(y-7)/(x+2)=(-12)/4
(y-7)/(x+2)=-3
cross multiply
y-7=-3(x+2)
y-7=-3x-6
y=-3x-6+7
y=-3x+1
31-+=16
28+b=50
33+c=54
52-n+=24
Answers
The solution to the equations are b = 15, b = 22, c = 21 and n = 28
How to determine the solution to the equationsFrom the question, we have the following equations that can be used in our computation:
31 - b = 16
28 + b = 50
33 + c = 54
52 - n = 24
Next, we collect the like terms in each of the equation
This gives
b = 31 - 16
b = 50 - 28
c = 54 - 33
n = 52 - 24
Lastly, we evaluate the like terms
b = 15
b = 22
c = 21
n = 28
The above are the solutions to the equations
Read more about equations at
https://brainly.com/question/148035
#SPJ1
Question
Solve the following equations:
31 - b = 16
28 + b = 50
33 + c = 54
52 - n = 24
Erika's toy is valued at €450. Its value increased by 10% then decreases by 10% the year after. What is the value of Erika's toy after these two changes?
Answers
Answer:
€445.50-------------------------
Initial value of the toy is €450.
After 10% increase the value is:
€450 + 10% = €450*1.1 = €495After further 10% decrease the value becomes:
€495 - 10% = €495*0.9 = €445.50The final value of the toy is €445.50.
Is 1/4 equal to 1/12
Answers
Answer: no
Step-by-step explanation:
First solution: 1/4 and 1/12 can be converted to decimals; 1/4 would be .25 and 1/12 would be .0833333
0.25 > 0.83333333
Second (simpler) solution: the larger the denominator, the less the numerator is worth
evaluate the function at the given value of the independent variable. simplify the results. (if an answer is undefined, enter undefined.)f(x) = 1/√(x-4)f(x) - f(5) / x - 5
Answers
The function at the given value of the independent variable, f(x) = 1/√(x-4)f(x) - f(5) / x - 5 is (x-5).
Each element of X is given precisely one element of Y by the function from a set X to a set Y. The sets X and Y are collectively referred to as the function's domain and codomain, respectively. Initially, functions represented the idealised relationship between two changing quantities.
We have given function as ,
f(x) = 1/√(x-4)
We have to find f(x) - f(5)/x-5
f(x) = f(5)/x-5 = 1/√(5-4)/(x-5)
= 1/√(5-4)/(x-5)
= (x-5)/√(5-4)
= (x-5)
Therefore, The function at the given value of the independent variable, f(x) = 1/√(x-4)f(x) - f(5) / x - 5 is (x-5).
Learn more about function:
https://brainly.com/question/29149836
#SPJ4
Please help!!
Thankyou!!

Answers
The scale factor is: 1.8
because of :
\(\frac{36}{20}=1.8\\ \\\\\frac{25.2}{14}=1.8\)
PLEASE ANSWER ASAP FOR BRAINLEST!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Answers
Answer:
D) 14 x Pi
Step-by-step explanation:
Answer:
\(14*\pi\)
Step-by-step explanation:
The equation for calculating the circumference of a circle is \(C=\pi D\) where C is the circumference and d is the diameter.
First, you would multiply the radius by 2 to find the diameter and place it into the equation to get your anwer:
\(14*\pi\)
Someone please help me with this question !!!!

Answers
Answer:
34.3 in, 36.3 in
Step-by-step explanation:
From the question given above, the following data were obtained:
Hypothenus = 50 in
1st leg (L₁) = L
2nd leg (L₂) = 2 + L
Thus, we can obtain the value of L by using the pythagoras theory as follow:
Hypo² = L₁² + L₂²
50² = L² + (2 + L)²
2500 = L² + 4 + 4L + L²
2500 = 2L² + 4L + 4
Rearrange
2L² + 4L + 4 – 2500 = 0
2L² + 4L – 2496 = 0
Coefficient of L² (a) = 2
Coefficient of L (n) = 4
Constant (c) = –2496
L = –b ± √(b² – 4ac) / 2a
L = –4 ± √(4² – 4 × 2 × –2496) / 2 × 2
L = –4 ± √(16 + 19968) / 4
L = –4 ± √(19984) / 4
L = –4 ± 141.36 / 4
L = –4 + 141.36 / 4 or –4 – 141.36 / 4
L = 137.36/ 4 or –145.36 / 4
L = 34.3 or –36.3
Since measurement can not be negative, the value of L is 34.3 in
Finally, we shall determine the lengths of the legs of the right triangle. This is illustrated below:
1st leg (L₁) = L
L = 34.4
1st leg (L₁) = 34.3 in
2nd leg (L₂) = 2 + L
L = 34.4
2nd leg (L₂) = 2 + 34.3
2nd leg (L₂) = 36.3 in
Therefore, the lengths of the legs of the right triangle are 34.3 in, 36.3 in
Can someone help me pls

Answers
Answer:
x=78
Step-by-step explanation:
q is 90 degrees since it is a right angle,
p=12
90 plus 12 =102
x=180-102
x=78
The jacket at the department store originally cost $199. It was selling so well that the store decided to increase the price by 25 percent. What was the new cost of the jacket?
Answers
Answer:
$248.75
Step-by-step explanation:
25% more of 199 is 248.75
B is the midpoint of AC.
If BC is 3x - 7 and AC is 9x - 61, what is the length of AB?
Answers
Answer:
The length of AB is 40
Step-by-step explanation:
The Midpoint of a Segment
If A and B are the endpoints of a segment, and C is the midpoint of AB, then the distance from A to C is equal to the distance from B to C.
We are given the lengths BC=3x-7 and AC=9x-61:
9x - 61 = 3x - 7
Subtracting 3x:
6x - 61 = - 7
Adding 61:
6x = 54
Dividing by 6:
x = 9
The total length AB is
BC+AC=3x - 7 + 9x - 61 = 12x - 68
Substituting x=9:
AB = 12*9 - 68 = 40
The length of AB is 40
Multiplicative inverse of 4/3
Answers
Answer:
The multiplicative inverse of 4/3 is 3/4. You literally swap the a and b points.
There are 30 students in a class of 18 of them own at least one pet what fraction of the class own pets? Give your answer in its simplest form
Answers
Answer:
18/30 simplified is 3/5
Step-by-step explanation:
Marcelo can select from 2 types of oranges and 3 types of peaches. If he randomly selects 1 orange and 1 peach, how many possible choices does he have? ___________ possible choices
Answers
2x3=6
oranges-
peaches-
possible combination:
1-
2-
3-
4-
5-
6-
The length of the longer leg of a 30 60 90 triangle is 6. The hyp is 9.
State the solution in Simple Root Form:
State the solution to the nearest tenth:
Answers
Step-by-step explanation:
there is something severely wrong with the problem definition.
when the Hypotenuse = 9, there is no 30-60-90 triangle with a leg = 6.
and when we are just focusing that this is a right-angled triangle with the Hypotenuse = 9, then 6 cannot be the longer leg.
it is also not clear what the solution is supposed to be. the 2nd leg ? the area ? the perimeter ? the height(s) ? ...
what ?
so, all I can do here is to show you why I said what I said :
30-60-90 triangle with Hypotenuse = 9
then the longer leg is opposite of the 60° angle and therefore sin(60)×9 = 7.794228634...
the shorter leg is opposite of the 30° angle and therefore sin(30)×9 = 0.5×9 = 4.5
a right-angled triangle with Hypotenuse = 9, one leg = 6 gives us per Pythagoras for the other leg
9² = 6² + leg²
81 = 36 + leg²
45 = leg²
leg = sqrt(45) = 6.708203932...
so, you see, as stated above, there is no leg with the length 6 in such a 30-60-90 triangle.
and in a more general right-angled triangle, if one leg = 6, then the other leg is actually longer.
therefore, there is everything wrong with the problem definition.
6. Journalise the following transactions
1. Bricks for Rs 60,000 and timber for Rs 35,000 purchased for
the construction of building. The payment was made by cheque.
2. Placed in fixed deposit account at bank by transfer from current
account Rs 13,000.
3. Appointed Mr. S.N. Rao as Accountant at Rs 300 p.m. and
Received Rs 1000 as security Deposit at 5% p.a. interest.
4. Sold goods to shruti for Rs 80,000 at 15% trade discount and
4% cash discount. Received 75% amount immediately through a
cheque.
5. Purchased goods from Richa for Rs 60,000 at 10% trade
discount and 5% cash discount. 60% amount paid by cheque
immediately.
6.
On 18th jan,Sold goods to shilpa at the list price of Rs 50,000
20% trade discount and 4% cash discount if the payment is made
within 7 days. 75% payment is received by cheque on Jan 23rd.
7. On 25th jan, sold goods to garima for Rs 1,00,000 allowed her
20% trade discount and 5% cash discount if the payment is made
within 15 days. She paid 1/4th of the amount by cheque on Feb 5th
and 60% of the remainder on 15th in cash.
8. Purchased land for Rs 2,00,000 and paid 1% as brokerage and
Rs 15,000 as registration charges on it. Entire payment is made by
cheque.
9. Goods worth Rs 25,000 and cash Rs 40,000 were taken away
by the proprietor for his personal use.
10. Sold goods costing Rs 1,20,000 to charu at a profit of 33% 3 %
on cost less 15% trade discount.
9
11. Paid rent of building Rs 60,000 by cheque. Half the building is
used by the proprietor for residential purpose.
12. Sold goods costing Rs 20,000 to sunil at a profit of 20% on
sales less 20% trade discount .
13. Purchased goods for Rs 1000 from nanda and supplied it to
helen for Rs 1300. Helen returned goods worth Rs 390, which in
turn were returned to nanda.
14. Received invoice at 10% trade discount from rohit and sons
and supplied these goods to madan, listed at Rs 3000.
Answers
1.Bricks and timber purchased for construction. (Debit: Bricks - Rs 60,000, Debit: Timber - Rs 35,000, Credit: Bank - Rs 95,000)
2.Transfer of Rs 13,000 to fixed deposit account. (Debit: Fixed Deposit - Rs 13,000, Credit: Current Account - Rs 13,000)
3.Appointment of Mr. S.N. Rao as Accountant. (Debit: Salary Expense - Rs 300, Debit: Security Deposit - Rs 1,000, Credit: Accountant - Rs 300)
4.Goods sold to Shruti with discounts. (Debit: Accounts Receivable - Shruti - Rs 80,000, Credit: Sales - Rs 80,000)
5.Goods purchased from Richa with discounts. (Debit: Purchases - Rs 60,000, Credit: Accounts Payable - Richa - Rs 60,000)
6.Goods sold to Shilpa with discounts and received payment. (Debit: Accounts Receivable - Shilpa - Rs 50,000, Credit: Sales - Rs 50,000)
7.Goods sold to Garima with discounts and received partial payment. (Debit: Accounts Receivable - Garima - Rs 1,00,000, Credit: Sales - Rs 1,00,000)
8.Purchase of land with additional charges. (Debit: Land - Rs 2,00,000, Debit: Brokerage Expense - Rs 2,000, Debit: Registration Charges - Rs 15,000, Credit: Bank - Rs 2,17,000)
9.Proprietor took goods and cash for personal use. (Debit: Proprietor's Drawings - Rs 65,000, Credit: Goods - Rs 25,000, Credit: Cash - Rs 40,000)
10.Goods sold to Charu with profit and discount. (Debit: Accounts Receivable - Charu - Rs 1,20,000, Credit: Sales - Rs 1,20,000)
11.Rent paid for the building. (Debit: Rent Expense - Rs 60,000, Credit: Bank - Rs 60,000)
12.Goods sold to Sunil with profit and discount. (Debit: Accounts Receivable - Sunil - Rs 24,000, Credit: Sales - Rs 24,000)
13.Purchased goods from Nanda and supplied to Helen. (Debit: Purchases - Rs 1,000, Debit: Accounts Payable - Nanda - Rs 1,000, Credit: Accounts Receivable - Helen - Rs 1,300, Credit: Sales - Rs 1,300)
14.Purchased goods from Rohit and Sons and supplied to Madan. (Debit: Purchases - Rs 2,700, Credit: Accounts Payable - Rohit and Sons - Rs 2,700, Debit: Accounts Receivable - Madan - Rs 3,000, Credit: Sales - Rs 3,000)
Here are the journal entries for the given transactions:
1. Bricks and timber purchased for construction:
Debit: Bricks (Asset) - Rs 60,000
Debit: Timber (Asset) - Rs 35,000
Credit: Bank (Liability) - Rs 95,000
2. Transfer to fixed deposit account:
Debit: Fixed Deposit (Asset) - Rs 13,000
Credit: Current Account (Asset) - Rs 13,000
3. Appointment of Mr. S.N. Rao as Accountant:
Debit: Salary Expense (Expense) - Rs 300
Debit: Security Deposit (Asset) - Rs 1,000
Credit: Accountant (Liability) - Rs 300
4. Goods sold to Shruti:
Debit: Accounts Receivable - Shruti (Asset) - Rs 80,000
Credit: Sales (Income) - Rs 80,000
5. Goods purchased from Richa:
Debit: Purchases (Expense) - Rs 60,000
Credit: Accounts Payable - Richa (Liability) - Rs 60,000
6. Goods sold to Shilpa:
Debit: Accounts Receivable - Shilpa (Asset) - Rs 50,000
Credit: Sales (Income) - Rs 50,000
7. Goods sold to Garima:
Debit: Accounts Receivable - Garima (Asset) - Rs 1,00,000
Credit: Sales (Income) - Rs 1,00,000
8.Purchase of land:
Debit: Land (Asset) - Rs 2,00,000
Debit: Brokerage Expense (Expense) - Rs 2,000
Debit: Registration Charges (Expense) - Rs 15,000
Credit: Bank (Liability) - Rs 2,17,000
9. Goods and cash taken away by proprietor:
Debit: Proprietor's Drawings (Equity) - Rs 65,000
Credit: Goods (Asset) - Rs 25,000
Credit: Cash (Asset) - Rs 40,000
10. Goods sold to Charu:
Debit: Accounts Receivable - Charu (Asset) - Rs 1,20,000
Credit: Sales (Income) - Rs 1,20,000
Credit: Cost of Goods Sold (Expense) - Rs 80,000
Credit: Profit on Sales (Income) - Rs 40,000
11. Rent paid for the building:
Debit: Rent Expense (Expense) - Rs 60,000
Credit: Bank (Liability) - Rs 60,000
12. Goods sold to Sunil:
Debit: Accounts Receivable - Sunil (Asset) - Rs 24,000
Credit: Sales (Income) - Rs 24,000
Credit: Cost of Goods Sold (Expense) - Rs 20,000
Credit: Profit on Sales (Income) - Rs 4,000
13. Goods purchased from Nanda and supplied to Helen:
Debit: Purchases (Expense) - Rs 1,000
Debit: Accounts Payable - Nanda (Liability) - Rs 1,000
Credit: Accounts Receivable - Helen (Asset) - Rs 1,300
Credit: Sales (Income) - Rs 1,300
14. Goods received from Rohit and Sons and supplied to Madan:
Debit: Purchases (Expense) - Rs 2,700 (after 10% trade discount)
Credit: Accounts Payable - Rohit and Sons (Liability) - Rs 2,700
Debit: Accounts Receivable - Madan (Asset) - Rs 3,000
Credit: Sales (Income) - Rs 3,000
for such more question on journal entries
https://brainly.com/question/28390337
#SPJ8
Grade 5 math. ! 30 points !
During the month of june, jessica volunteers at a library every 6 days and at a veterinarians office every 10 days. jessica’s first visit to the library was on June 6 and her first visit to the veterinarian office was on June 1th.
What day in June will jessica volunteer at both locations?
Anwser Options
june 6
june 10
june 18
june 20
june 24
june 30
Answers
The day in June, Jessica volunteered at both locations if she volunteers at the library every 6 days and at a veterinarian's office every 10 days is June 30, so option F is correct.
What is LCM?The abbreviation LCM stands for "Least Common Multiple." The smallest multiple that two or more numbers share is known as the least common multiple.
For instance: The LCM of 2 and 3 is 6.
Given:
Jessica volunteers library every 6 days,
Jessica's veterinarian's office, every 10 days,
So for her visit to both, the place takes the LCM of 6 and 10,
LCM of 6 and 10 = 30,
Hence, on the 30th day, she visits both places so if she starts volunteering from the 1st of June then she will visit both places on the 30th of June.
Therefore, The day in June, Jessica volunteered at both the location if she volunteers at a library every 6 days and at a veterinarian's office every 10 days. Jessica’s first visit to the library was on June 6 and her first visit to the veterinarian's office was on June, 1st is June 30.
To know more about LCM:
https://brainly.com/question/20739723
#SPJ2
Answer:June 30th
Step-by-step explanation:
So Jessica volunteers every 6 days and 10 days at different places.From June 6th and June 1st you see which one is good for both of them and then June 30th is the answer.
3. A pound of flour costs $12. How many ounces of flour can be purchased for $3.30?
Answers
With a pound of flour costing $12 and considering that there are 16 ounces in a pound, the cost per ounce is $0.75. Thus, for $3.30, you can purchase 4.4 ounces of flour.
To find out how many ounces of flour can be purchased for $3.30, we need to determine the cost of one ounce of flour.
Given that a pound of flour costs $12, we know that there are 16 ounces in a pound (since there are 16 ounces in 1 pound). So, the cost of one ounce of flour can be calculated as:
Cost of one ounce of flour = Cost of one pound of flour / Number of ounces in one pound
Cost of one ounce of flour = $12 / 16 ounces
Cost of one ounce of flour = $0.75
Therefore, the cost of one ounce of flour is $0.75.
To determine how many ounces of flour can be purchased for $3.30, we divide the total amount of money by the cost of one ounce of flour:
Number of ounces of flour = Total money / Cost of one ounce of flour
Number of ounces of flour = $3.30 / $0.75
Number of ounces of flour ≈ 4.4 ounce
Therefore, for $3.30, approximately 4.4 ounces of flour can be purchased.
In summary, with the given cost of $12 for a pound of flour, and knowing that there are 16 ounces in a pound, we find that one ounce of flour costs $0.75. Thus, for $3.30, approximately 4.4 ounces of flour can be purchased.
for more such question on costing visit
https://brainly.com/question/25109150
#SPJ8